алгебра
19.01.2021
19.01.2021
12.01.2021Завдання на Мій клас
16.03.2020
Тема: Сума n перших членів геометрічноґ прогресії
З новим матеріалом ві можете ознайомитися за посиланнями:
Обов'язково робимо конспект у зошиті та опрацьовуємо параграф 17
виконуємо вправи 723 і 724
Додому беремо вправу 727
18.03.2020
Тема: Сума n перших членів геометрічноґ прогресії
виконуємо вправи 725 і 726
Додому беремо вправу 738
Задачі на обчислення сум
Опрацювати параграф 18 підручника, зробити короткий конспект, виконати вправи №761, 762, 765
Контрольна робота
Виконуємо контрольну роботу на подвійному аркуші, за тим варіантом. що сидите в школі. Приносите виконані роботи по закінченню карантину. /uploads/editor/2006/170823/sitepage_96/files/20168.docx
Тема: Основні правила комбінаторики
З підручника розвязуємо вправи №803,806,807,809,811,813
Чекаю на роботи!
Новий матеріал за посиланням https://www.youtube.com/watch?v=NOHGl5wwSnI
або за параграфом 20 підручника
Складаємо короткий конспект, розв'язуємо вправи №822-825(усно), №826,827,828,831,823,833,835(письмово).
Дивимося відео уроки на каналі Рада або UA:Культура з 10.00
Дивимося відео уроки на каналі Рада або UA:Культура з 10.00
Тести: https://naurok.com.ua/test/join
Код доступу 762154
Виконати вправи №836,838,839,841,843,844
1. Новий матеріал за посиланням https://www.youtube.com/watch?v=agTeiKu6VrQ
або параграф 21, короткий конспект
2. №855,857,860
3. Тести https://naurok.com.ua/test/join до 16.04.2020
Код доступу 977854
1. Новий матеріал за посиланням ПРЕЗЕНТАЦІЯ або параграф 21
2. №861,862,863
3. https://miyklas.com.ua/ (2 шт.)
Виконуємо контрольну роботу на подвійному аркуші, фото, виконаної к.р. скидаємо мені в особисті повідомлення.
Повторюємо матеріал за посиланням: https://subject.com.ua/mathematics/zno_2017/5.html
Робимо короткий конспект
Виконуємо тести https://naurok.com.ua/test/join
Код доступу 356200
Домашнє завдання ст.239 №871,873,875,877
Повторити лінійні рівняння, квадратні рівняння, способи розв'язування систем рівнянь
Виконати вправи №923,926.927,,928,930 по одному завданню з кожного номера на свій вибір.
Виконати тести https://naurok.com.ua/test/join
Код доступу 563090
Повторити формули скороченого множення
Виконати вправи №899, 902, 903
Виконати тести https://naurok.com.ua/test/join
Код доступу 637325
Схема 1
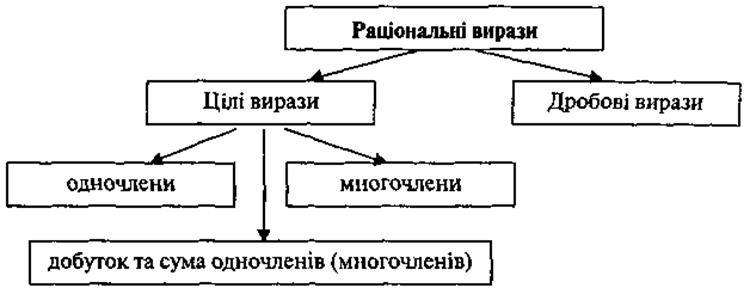
Схема 2
Схема 3
| Степінь з натуральним показником | |
|
|
|
| Для будь-яких x, y і додатних a і b справедливі рівності: a·a·a·...·a=ax; a0=1; a1=a; |
Схема 4
Виконати тести https://naurok.com.ua/test/join
Код доступу 797886
Квадратний корінь. Арифметичний квадратний корінь.
Рівняння х2 = а
Квадратним коренем із числа a називається число, квадрат якого дорівнює a.
Арифметичним квадратним коренем із числа a називається невід’ємне число, квадрат якого дорівнює a. Читаємо — «корінь квадратний з a».Знаком арифметичного квадратного кореня слугує радикал 
. Число a називається підкореневим виразом (
).
Не існує кореня квадратного з від’ємного числа.
Якщо корінь квадратний із числа a має смисл, то квадрат цього кореня дорівнює самому числу a:
.
Корінь квадратний із нуля дорівнює нулю: 
.
Історичні відомості
Поняття квадратного кореня з чисел відоме ще з часів стародавніх Вавилону та Єгипту, де були знайдені правила для їх наближеного обчислення.
Щоб розв’язати рівняння х2 = а, скористаємося спочатку графічним способом.
Для графічного розв’язання рівняння х2 = а необхідно побудувати графік функції y = x2 і графік функції y = a. Абсциси точок перетину побудованих графіків будуть розв’язками рівняння.
Кількість розв’язків залежить від положення прямої y = а, яка паралельна осі абсцис.
Якщо a від’ємне, то пряма лежить у третій і четвертій координатних чвертях і не перетинає параболу. Тоді рівняння розв’язків не має.
Якщо a дорівнює нулю, то пряма співпадає з віссю абсцис. Тоді рівняння має один розв’язок x = 0.
Якщо a додатне, то пряма лежить у першій і другій координатних чвертях і перетинає параболу у двох точках. Тоді рівняння має два розв’язки — 
і 
.
Для аналітичного способу розв’язання рівняння х2 = а запам’ятайте:
1) якщо а — від’ємне число, рівняння коренів не має;
2) якщо а дорівнює нулю, то корінь рівняння — нуль;
3) якщо а — число додатне, то рівняння має два корені — і.
Арифметичний квадратний корінь із добутку, дробу і степеня. Добуток і частка квадратних коренів. Тотожність 
Корінь квадратний із добутку невід’ємних множників дорівнює добутку коренів квадратних із цих множників: 
. Добуток коренів квадратних із невід’ємних чисел дорівнює кореню квадратному з добутку підкореневих виразів.
Корінь квадратний із дробу, чисельник якого невід’ємний, а знаменник додатний, дорівнює кореню квадратному з чисельника дробу, поділеному на корінь квадратний зі знаменника дробу: 
. Частка коренів квадратних із додатних чисел дорівнює кореню квадратному з частки підкореневих виразів.
Корінь квадратний зі степеня невід’ємного числа дорівнює степеню цього числа з показником, удвічі меншим за даний: 
. N-ий степінь кореня квадратного з числа a дорівнює кореню квадратному з n-ого степеня підкореневого виразу: 
.
Корінь із квадрата будь-якого числа дорівнює модулю цього числа: 
.
Модуль будь-якого виразу дорівнює кореню квадратному з квадрата цього виразу.
Тотожні перетворення виразів, що містять квадратні корені
1) Винесення множника з-під знака кореня
Якщо задано квадратний корінь із добутку, що містить множники, які є парними степенями змінних, то такі множники можна виносити з-під знака кореня. При цьому одержимо добуток модуля цього множника у степені, удвічі меншому за даний, на корінь квадратний із множників із непарними показниками степеня.
Якщо показник степеня деякого множника непарний, але більший за три, то його можна розкласти на множники, які є степенями з тією ж основою і показниками, що в сумі дорівнюють заданому показнику степеня.
Зверніть увагу!
Треба слідкувати, щоб вираз, який залишається під коренем, був невід’ємним.
2) Внесення множника під знак кореня
Якщо дано вираз, що є добутком множників, деякі з яких не знаходяться під коренем квадратним, то такі множники можна внести під знак кореня множником, степінь якого буде вдвічі більшим за даний.
3) Звільнення від ірраціональності в знаменнику дробу
Щоб звільнитися від ірраціональності в знаменнику дробу, треба чисельник і знаменник помножити на вираз, спряжений зі знаменником. При цьому враховуйте, що:
- для кореня квадратного з числа a спряженим буде корінь квадратний із числа a;
- для суми коренів квадратних із чисел a і b спряженим буде різниця коренів квадратних із чисел a і b 
;
для різниці коренів квадратних із чисел a і b спряженим буде сума коренів квадратнихі з чисел a і b 
.
Виконати тести https://naurok.com.ua/test/join
Код доступу 512140
Повторити основні задачі на відсотки, виконати конспект в робочому зошиті
Завдання виконуємо на подвійному аркуші і скидаємо у вайбер в особисті повідомлення
Підписуємо:
Семестрова контрольна робота
з алгебри
учня/учениці 9 класу
ПІБ(в р. в.)
Бажаю успіхів!
Виконати тести https://naurok.com.ua/test/join
Код доступу 4004656
